It's important to emphasize that "realistic-looking" data does *not* mean "realistic" data – especially high-dimensional data (unfortunately that post doesn't warn against this).
If one had an algorithm that generated realistic data for a given inference problem, it would mean that that inference problem had been solved. So: for educational purposes, why not. But for validation-like purposes, use with uttermost caution and at your own peril.
The bayesEO package provides a Bayesian approach to post-processing ML-generated images. It refines class probabilities, removes outliers, and improves labeling for more accurate classification.
Байесовская собака: анализ пёсьего компаса
Ориентируются ли собаки по компасу, когда делают свои грязные дела? Оказывается — да! Если вам интересно, как можно это подтвердить в домашних условиях, используя компас, Байесовскую статистику и собаку (собака не включена), то добро пожаловать под кат.
Happy Birthday, Laplace! 
One of the first to use Bayesian probability theory in the modern way!
"One sees in this essay that the theory of probabilities is basically only common sense reduced to a calculus. It makes one estimate accurately what right-minded people feel by a sort of instinct, often without being able to give a reason for it. It leaves nothing arbitrary in the choice of opinions and of making up one's mind, every time one is able, by this means, to determine the most advantageous choice. Thereby, it becomes the most happy supplement to ignorance and to the weakness of the human mind. If one considers the analytical methods to which this theory has given rise, the truth of the principles that serve as the groundwork, the subtle and delicate logic needed to use them in the solution of the problems, the public-benefit businesses that depend on it, and the extension that it has received and may still receive from its application to the most important questions of natural philosophy and the moral sciences; if one observes also that even in matters which cannot be handled by the calculus, it gives the best rough estimates to guide us in our judgements, and that it teaches us to guard ourselves from the illusions which often mislead us, one will see that there is no science at all more worthy of our consideration, and that it would be a most useful part of the system of public education."
*Philosophical Essay on Probabilities*, 1814 <https://doi.org/10.1007/978-1-4612-4184-3>
After a long collaboration with @martinbiehl, @mc and @Nathaniel I’m excited to share the first of (hopefully) many outputs:
“A Bayesian Interpretation of the Internal Model Principle”
https://arxiv.org/abs/2503.00511.
This work combines ideas from control theory, applied #categorytheory and #Bayesian reasoning, with ramifications for #cognitive science, #AI/#ML, #ALife and biology to be further explored in the future.
In these fields, we come across ideas of “models”, “internal models”, “world models”, etc. but it is hard to find formal definitions, and when one does, they usually aren’t general enough to cover all the aspects these different fields consider important.
In this work, we focus on two specific definitions of models, and show their connections. One is inspired by work in control theory, and one comes from Bayesian inference/filtering for cognitive science, AI and ALife, and is formalised with Markov categories.
In the first part, we review and reformulate the “internal model principle” from control theory (at least, one of its versions) in a more modern language heavily inspired by categorical systems theory (https://www.davidjaz.com/Papers/DynamicalBook.pdf, https://github.com/mattecapu/categorical-systems-theory/blob/master/main.pdf).
6/ Thus we built upon this #Bayesian framework (https://doi.org/10.1038/s41467-021-24149-x) to infer each pairwise interaction in individual-based #networks accounting for sampling effort and the inherent stochasticity of field data
A #bayesian blogpost, by two of my undergraduate students! It's their report on their learning Bayesian modeling by applying it to my lab's data.
https://alexholcombe.github.io/brms_psychometric_variableGuessRate_lapseRate/DenisonBlog.html
Summary: we learned to use brms. But had trouble when we added more than one or two factors to the model. Little idea why; haven't had time to tinker much with that.
I'm explaining Hamiltonian Monte Carlo in my grad-level stats class tomorrow, so I put together this animation illustrating HMC in one dimension. I find it very soothing.
Got the physical copies of my Cambridge element in the mail. A reminder that the whole book is free to download until the end of February: https://doi.org/10.1017/9781009210171
GO GO GO! We're live next week in 40 George Square, #Edinburgh
Come and hear Isabella and Jordan talk about #Bayesian #Statistics in #RStats
Details: http://edinbr.org/edinbr/2025/02/17/February-meeting.html
The revised paper "The ARR2 prior: flexible predictive prior definition for Bayesian auto-regressions" with David Kohns, Noa Kallioinen, Yann McLatchie adds results about implied priors on characteristic roots and partial autocorrelations, case study with quasi-cyclical behavior, and extensions to MA, ARMA, ARDL, and VAR models.
If I collect some data for a new treatment, but don't collect a control group, can I use the data from an older study that has the control condition? If so, how would I integrate this into my analysis? and what is the name for this? historical control?
Today at #WorkshopsForUkraine: Structural Equation Models and the Do-Operator in PyMC, by Nathaniel Forde (Personio), February 6th, 6 pm CET (PyMC is "a probabilistic programming library for #Python that allows users to build #Bayesian models with a simple Python API and fit them using Markov chain Monte Carlo (MCMC) methods"). Register or sponsor a place for a student by donating to support #Ukraine. Details: https://sites.google.com/view/dariia-mykhailyshyna/main/r-workshops-for-ukraine#h.d5fce3wbt3kr
'Approximate Bayesian inference from noisy likelihoods with Gaussian process emulated MCMC', by Marko Järvenpää, Jukka Corander.
http://jmlr.org/papers/v25/21-0421.html
#mcmc #bayesian #likelihoods
"A p-value is an #estimate of p(Data | Null Hypothesis). " – not correct. A p-value is an estimate of
p(Data or other imagined data | Null Hypothesis)
so not even just of the actual data you have. Which is why p-values depend on your stopping rule (and do not satisfy the "likelihood principle"). In this regard, see Jeffreys's quote below.
Imagine you design an experiment this way: "I'll test 10 subjects, and in the meantime I apply for a grant. At the time the 10th subject is tested, I'll know my application's outcome. If the outcome is positive, I'll test 10 more subjects; if it isn't, I'll stop". Not an unrealistic situation.
With this stopping rule, your p-value will depend on the probability that you get the grant. This is not a joke.
"*What the use of P implies, therefore, is that a hypothesis that may be true may be rejected because it has not predicted observable results that have not occurred.* This seems a remarkable procedure. On the face of it the fact that such results have not occurred might more reasonably be taken as evidence for the law, not against it." – H. Jeffreys, "Theory of Probability" § VII.7.2 (emphasis in the original) <https://doi.org/10.1093/oso/9780198503682.001.0001>.
What do you answer when a statistician asks you whether Bayesian methods are "sanctioned" or "legitimate" or "established" or similar?
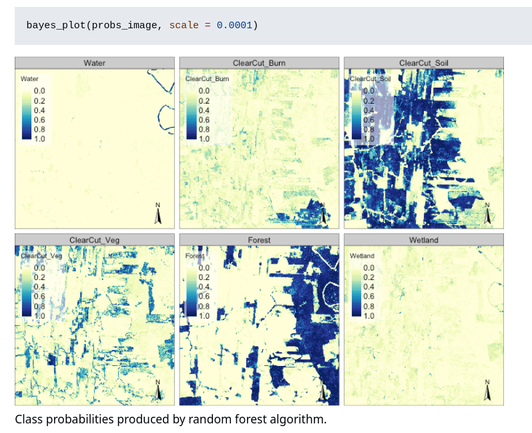
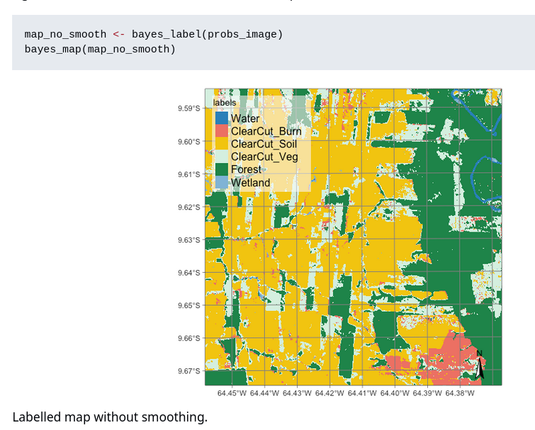
We have a paper that tries to introduce clinicians (and people working with machine learning), in a very friendly way and with a concrete example, to Bayesian methods. More precisely to "Bayesian nonparametric population inference" (also called "nonparametric exchangeable inference" or "nonparametric density regression"):
https://doi.org/10.31219/osf.io/8nr56
The paper guides the clinician from the hypothetical problem of predicting Alzheimer onset in four patients, given some predictors from each patient and previous trials, to the (again hypothetical) problem of deciding upon a treatment.
This method allows for a quantitative and yet intuitively understandable assessment of hypotheses, even when the hypotheses come in degrees rather than as artificial binary pairs. And it has further advantages:
- It's "model-free", in the sense that it doesn't make specific assumptions (such as gaussianity, linearity, and similar).
- It quantifies how much the results could change if the clinician had more trial data. That is, it quantifies the uncertainty coming from finite sample size.
- It works with small or large sample sizes alike.
- It can quantify (again in a model-free way) the importance of different predictors.
- It does imputation of data in a principled, exact way.
- It can account for and correct inappropriate base rates and similar biases.
- It is fully integrated with Clinical Decision Making (see eg the textbooks like Sox & al <https://doi.org/10.1002/9781118341544> or Hunink & al <https://doi.org/10.1017/CBO9781139506779>)
The text is addressed to clinicians, statisticians, and researchers in machine learning. The emphasis is on the understanding of the ideas involved, rather than on the maths.
If you have the time to take a look and if you find it valuable, then I'd be thankful if you boosted this reach-out post. Also happy to receive comments about unclear passages and errors of course.
Cheers!
